简单

问题描述

给出一棵二叉树，其上每个结点的值都是 0 或 1 。每一条从根到叶的路径都代表一个从最高有效位开始的二进制数。

• 例如，如果路径为 0 -> 1 -> 1 -> 0 -> 1，那么它表示二进制数 01101，也就是 13 。

对树上的每一片叶子，我们都要找出从根到该叶子的路径所表示的数字。

返回这些数字之和。题目数据保证答案是一个 32 位 整数。

示例 1：

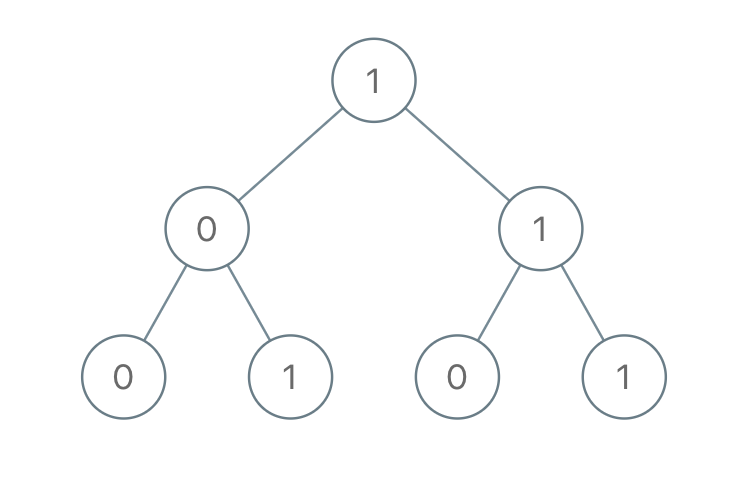
输入：root = [1,0,1,0,1,0,1]
输出：22
解释：(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22

示例 2：

输入：root = [0]
输出：0

提示：

• 树中的节点数在 [1, 1000] 范围内
• Node.val 仅为 0 或 1

递归

递归求解是比较容易理解的方法，在 $\text {DFS}$ 过程中记录当前值为多少，操作方法为将当前记录值左移 $1$ 位，然后加上当前节点的值。遇到根节点时，将根节点计算到的值加入到求和结果中，最终返回所有根节点的和。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var sumRootToLeaf = function (root) {
  let sum = 0
  const dfs = (node, val) => {
    if (!node) return
    val = (val << 1) | node.val
    if (!node.left && !node.right) sum += val
    dfs(node.left, val)
    dfs(node.right, val)
  }
  dfs(root, 0)
  return sum
}

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$（递归栈空间）

迭代

迭代需要使用栈去模拟递归过程。

进行一次树的后序遍历，每次入栈，我们都进行一次计算，记录当前位置上的值，出栈时，如果是根节点，则将当前位置值加入到求和结果中，然后右移 $1$ 位，将位置回退到父节点。

可以发现，实际上，某一个节点在路径上的值是固定的，我们可以在迭代过程中，对当前遍历到的节点的值修改为它在路径上的值，每次出栈就能得到当前位置上的值了，直接对根节点值进行累计即可得到答案。

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$