中等

问题描述

给你一个数组 points ，其中 points[i] = [xi, yi] ，表示第 i 个点在二维平面上的坐标。多个点可能会有 相同 的坐标。

同时给你一个数组 queries ，其中 queries[j] = [xj, yj, rj] ，表示一个圆心在 (xj, yj) 且半径为 rj 的圆。

对于每一个查询 queries[j] ，计算在第 j 个圆 内 点的数目。如果一个点在圆的 边界上 ，我们同样认为它在圆 内 。

请你返回一个数组 answer ，其中 answer[j] 是第 j 个查询的答案。

示例 1：

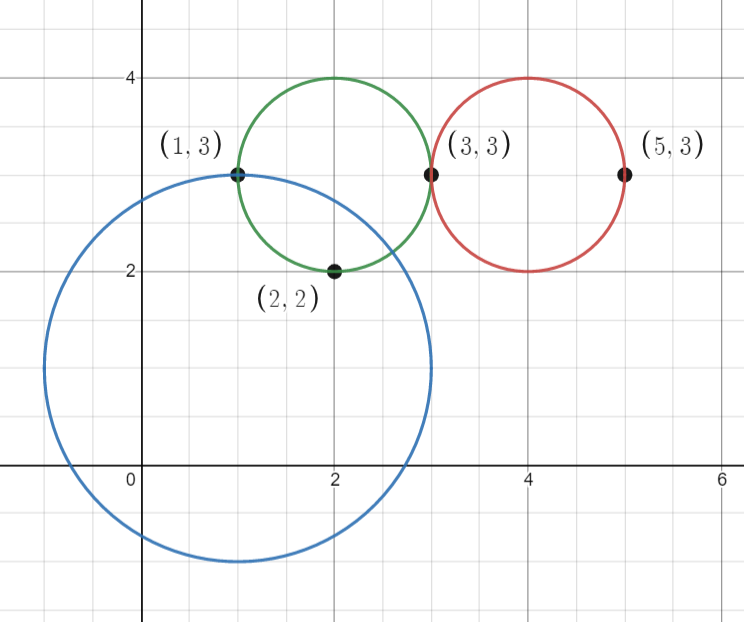
输入：points = [[1,3],[3,3],[5,3],[2,2]], queries = [[2,3,1],[4,3,1],[1,1,2]]
输出：[3,2,2]
解释：所有的点和圆如上图所示。
queries[0] 是绿色的圆，queries[1] 是红色的圆，queries[2] 是蓝色的圆。

示例 2：

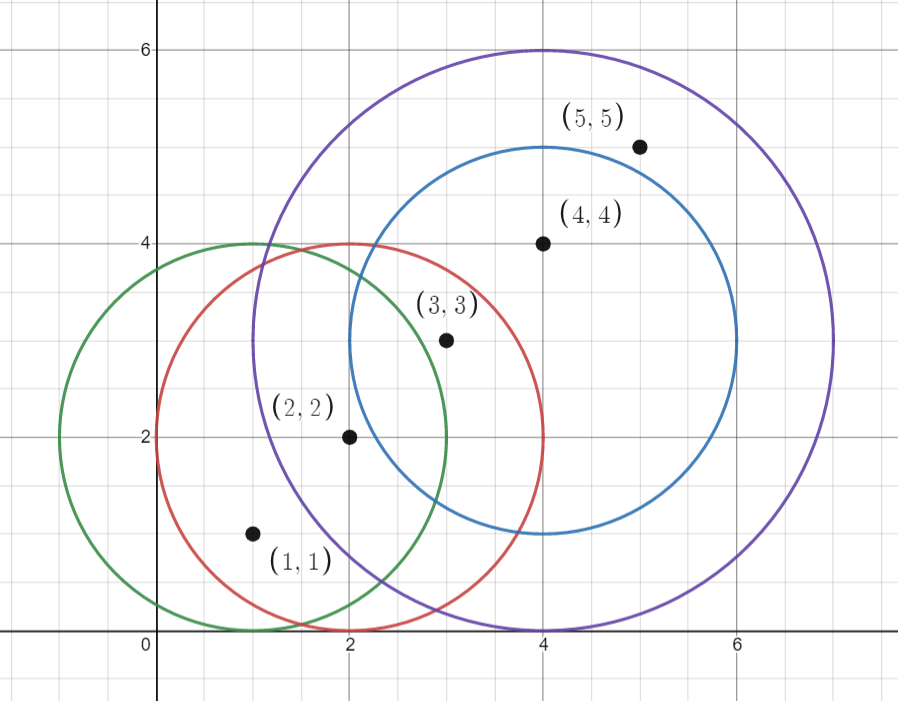
输入：points = [[1,1],[2,2],[3,3],[4,4],[5,5]], queries = [[1,2,2],[2,2,2],[4,3,2],[4,3,3]]
输出：[2,3,2,4]
解释：所有的点和圆如上图所示。
queries[0] 是绿色的圆，queries[1] 是红色的圆，queries[2] 是蓝色的圆，queries[3] 是紫色的圆。

提示：

• 1 <= points.length <= 500
• points[i].length == 2
• 0 <= xi, yi <= 500
• 1 <= queries.length <= 500
• queries[j].length == 3
• 0 <= xj, yj <= 500
• 1 <= rj <= 500
• 所有的坐标都是整数。

枚举

遍历每个查询，对于每个查询的点 $(x_i, y_i)$，遍历圆数组得到当前圆的圆心 $(x_j, y_j)$ 以及圆心 $r$，若：

$$(x_i - x_j)^2 + (y_i - y_j)^2 \leq r^2$$

则说明点在当前圆内，统计值自增即可。

/**
 * @param {number[][]} points
 * @param {number[][]} queries
 * @return {number[]}
 */
var countPoints = function (points, queries) {
  const n = queries.length
  const ans = new Array(n).fill(0)
  for (let i = 0; i < n; i++) {
    const [x1, y1, r] = queries[i]
    for (const [x2, y2] of points) {
      if ((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) <= r * r) {
        ans[i]++
      }
    }
  }
  return ans
}

• 时间复杂度：$O(n \times m)$
• 空间复杂度：$O(1)$