中等

问题描述

给你一棵二叉树的根节点 root ，请你构造一个下标从 0 开始、大小为 m x n 的字符串矩阵 res ，用以表示树的 格式化布局 。构造此格式化布局矩阵需要遵循以下规则：

• 树的 高度 为 height ，矩阵的行数 m 应该等于 height + 1 。
• 矩阵的列数 n 应该等于 2height+1 - 1 。
• 根节点 需要放置在 顶行 的 正中间 ，对应位置为 res[0][(n-1)/2] 。
• 对于放置在矩阵中的每个节点，设对应位置为 res[r][c] ，将其左子节点放置在 res[r+1][c-2height-r-1] ，右子节点放置在 res[r+1][c+2height-r-1] 。
• 继续这一过程，直到树中的所有节点都妥善放置。
• 任意空单元格都应该包含空字符串 "" 。

返回构造得到的矩阵 res 。

示例 1：

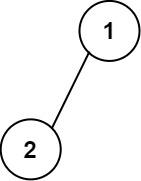
输入：root = [1,2]
输出：
[["","1",""],
 ["2","",""]]

示例 2：

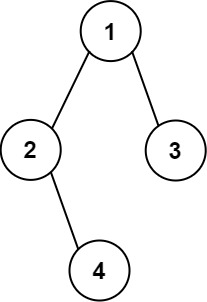
输入：root = [1,2,3,null,4]
输出：
[["","","","1","","",""],
 ["","2","","","","3",""],
 ["","","4","","","",""]]

提示：

• 树中节点数在范围 [1, 210] 内
• -99 <= Node.val <= 99
• 树的深度在范围 [1, 10] 内

深度优先搜索

先对树执行一次深度优先搜索，确定树的高度，然后按规则创建矩阵，再执行一次深度优先搜索，按照规则对数组内容进行填充。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {string[][]}
 */
var printTree = function (root) {
  let height = 0
  const dfs = (node, level) => {
    if (!node) return
    dfs(node.left, level + 1)
    dfs(node.right, level + 1)
    height = Math.max(height, level)
  }
  dfs(root, 1)
  const n = Math.pow(2, height)
  const ans = new Array(height).fill(0).map(() => new Array(n - 1).fill(''))
  const mapping = (node, level, pos) => {
    if (!node) return
    mapping(node.left, level + 1, pos - Math.pow(2, height - level - 1))
    mapping(node.right, level + 1, pos + Math.pow(2, height - level - 1))
    ans[level - 1][pos] = node.val.toString()
  }
  mapping(root, 1, (n - 1) >> 1)
  return ans
}

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$