简单

问题描述

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在**「杨辉三角」**中，每个数是它左上方和右上方的数的和。

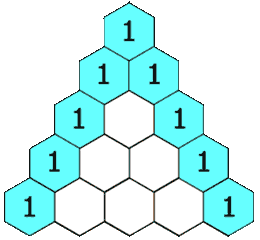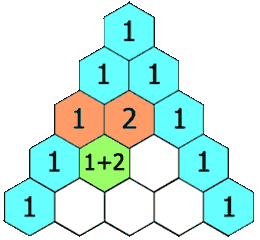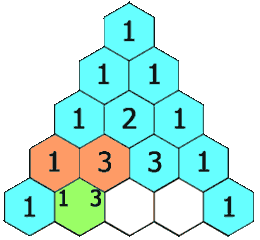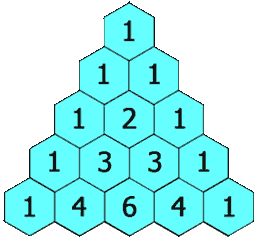
示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

输入: numRows = 1
输出: [[1]]

提示:

• 1 <= numRows <= 30

动态规划

假设层数为 $i$，那么第 $i$ 层就有 $i$ 个元素，且首尾是 $1$，假设 $dp[i][j]$ 表示第 $i$ 层，第 $j$ 个数，那么对于 $i > 0$， $0 < j < i$ 就有： $dp[i][j] = dp[i-1][j-1] + dp[i-1][j]$。

/**
 * @param {number} numRows
 * @return {number[][]}
 */
var generate = function (numRows) {
  const dp = []
  dp[0] = [1]
  for (let i = 1; i < numRows; i++) {
    dp[i] = [1]
    for (let j = 1; j < i; j++) {
      dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]
    }
    dp[i][i] = 1
  }
  return dp
}

• 时间复杂度：$O(n^2)$。
• 空间复杂度：$O(1)$，不考虑返回值的空间占用。