中等

问题描述

给你一个长度为 n 的 3 跑道道路 ，它总共包含 n + 1 个 点 ，编号为 0 到 n。一只青蛙从 0 号点第二条跑道 出发 ，它想要跳到点 n 处。然而道路上可能有一些障碍。

给你一个长度为 n + 1 的数组 obstacles，其中 obstacles[i]（取值范围从 0 到 3）表示在点 i 处的 obstacles[i] 跑道上有一个障碍。如果 obstacles[i] == 0，那么点 i 处没有障碍。任何一个点的三条跑道中 最多有一个 障碍。

• 比方说，如果 obstacles[2] == 1，那么说明在点 2 处跑道 1 有障碍。

这只青蛙从点 i 跳到点 i + 1 且跑道不变的前提是点 i + 1 的同一跑道上没有障碍。为了躲避障碍，这只青蛙也可以在 同一个 点处 侧跳 到 另外一条 跑道（这两条跑道可以不相邻），但前提是跳过去的跑道该点处没有障碍。

• 比方说，这只青蛙可以从点 3 处的跑道 3 跳到点 3 处的跑道 1 。

这只青蛙从点 0 处跑道 2 出发，并想到达点 n 处的 任一跑道 ，请你返回 最少侧跳次数 。

注意：点 0 处和点 n 处的任一跑道都不会有障碍。

示例 1：

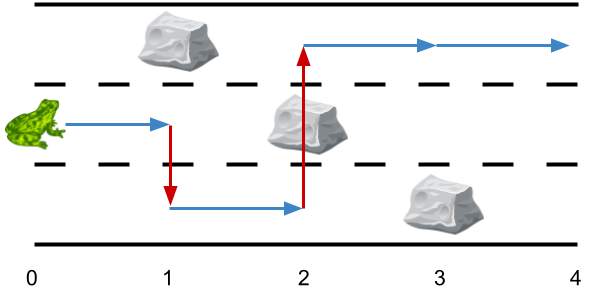
输入：obstacles = [0,1,2,3,0]
输出：2
解释：最优方案如上图箭头所示。总共有 2 次侧跳（红色箭头）。
注意，这只青蛙只有当侧跳时才可以跳过障碍（如上图点 2 处所示）。

示例 2：

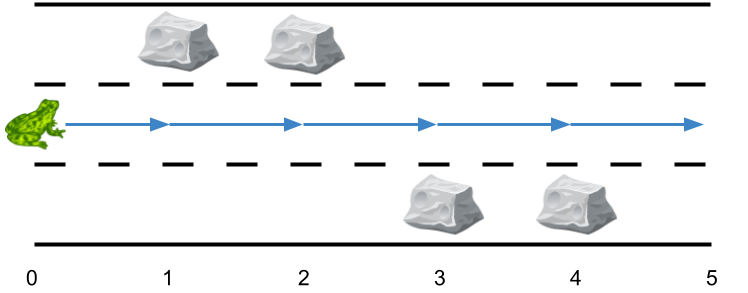
输入：obstacles = [0,1,1,3,3,0]
输出：0
解释：跑道 2 没有任何障碍，所以不需要任何侧跳。

示例 3：

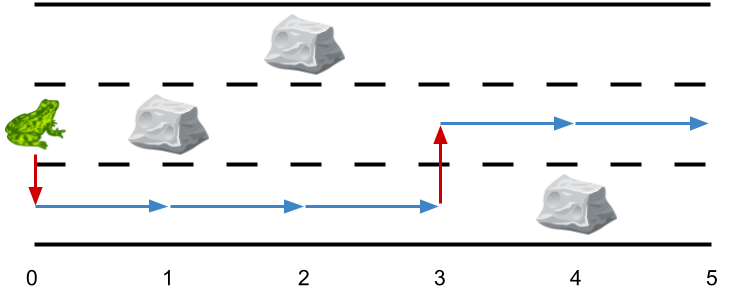
输入：obstacles = [0,2,1,0,3,0]
输出：2
解释：最优方案如上图所示。总共有 2 次侧跳。

提示：

• obstacles.length == n + 1
• 1 <= n <= 5 * 105
• 0 <= obstacles[i] <= 3
• obstacles[0] == obstacles[n] == 0

动态规划

假设 $dp[i][j]$ 为到达第 $i$ 个点，第 $j$ 条跑道的最少侧条次数，那么若该点没有障碍物，即 $obstacles[i] - 1 \neq j$，该点就能到达，可以到达的方式有在 $dp[i - 1][j]$ 不用侧跳直接过去，或者从其他跑道侧跳一次过去，只需取各种情况的最小值即可。由于 $dp[i][j]$ 仅由上一个状态转移，因此可以使用滚动数组优化空间。

/**
 * @param {number[]} obstacles
 * @return {number}
 */
var minSideJumps = function (obstacles) {
  const n = obstacles.length
  const dp = [1, 0, 1]
  for (let i = 1; i < n; i++) {
    const obstacle = obstacles[i] - 1
    dp[0] = obstacle !== 0 ? dp[0] : Infinity
    dp[1] = obstacle !== 1 ? dp[1] : Infinity
    dp[2] = obstacle !== 2 ? dp[2] : Infinity
    if (obstacle !== 0) dp[0] = Math.min(dp[0], Math.min(dp[1], dp[2]) + 1)
    if (obstacle !== 1) dp[1] = Math.min(dp[1], Math.min(dp[0], dp[2]) + 1)
    if (obstacle !== 2) dp[2] = Math.min(dp[2], Math.min(dp[0], dp[1]) + 1)
  }
  return Math.min(...dp)
}

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$