困难

问题描述

你打算利用空闲时间来做兼职工作赚些零花钱。

这里有 n 份兼职工作，每份工作预计从 startTime[i] 开始到 endTime[i]结束，报酬为profit[i]`。

给你一份兼职工作表，包含开始时间 startTime，结束时间 endTime 和预计报酬 profit 三个数组，请你计算并返回可以获得的最大报酬。

注意，时间上出现重叠的 2 份工作不能同时进行。

如果你选择的工作在时间 X 结束，那么你可以立刻进行在时间 X 开始的下一份工作。

示例 1：

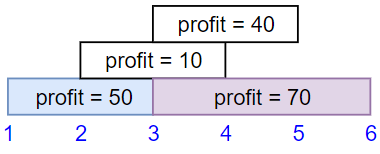
输入：startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
输出：120
解释：
我们选出第 1 份和第 4 份工作，
时间范围是 [1-3]+[3-6]，共获得报酬 120 = 50 + 70。

示例 2：

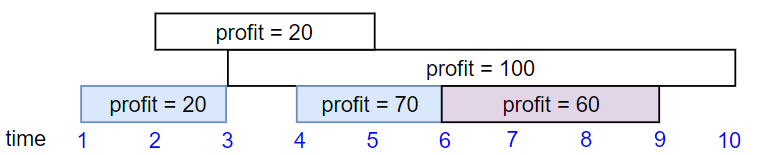
输入：startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
输出：150
解释：
我们选择第 1，4，5 份工作。
共获得报酬 150 = 20 + 70 + 60。

示例 3：

输入：startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
输出：6

提示：

• 1 <= startTime.length == endTime.length ==profit.length<= 5 * 10^4
• 1 <=startTime[i] <endTime[i] <= 10^9
• 1 <=profit[i] <= 10^4

动态规划 + 二分查找

以三元组 $[startTime, endTime, profit]$ 的形式表示一份兼职工作，然后将其按结束时间排序。对于某份兼职工作，有 选择 和 不选择 两种决策。 定义 $dp[i]$ 表示考虑前 $i$ 份工作时的最大收益（$i$ 从 $1$ 开始）：

• 不选择第 $i$ 份工作时，$dp[i] = dp[i - 1]$
• 选择第 $i$ 份工作时，由于第 $i$ 份工作开始时可能存在时间上的冲突，因此需要再前 $i$ 份工作中找出第 $k$ 份工作使得能够允许第 $i$ 份工作开始。那么此时选择完前 $k$ 份工作后，就能够选择第 $i$ 份工作。$dp[i] = dp[k] + jobs[i][2]$

那么可以得到状态转移方程:

$$dp[i] = Max(dp[i-1], dp[k] + jobs[i][2])$$

由于工作已按结束时间排序，因此查找是可以使用二分查找。

/**
 * @param {number[]} startTime
 * @param {number[]} endTime
 * @param {number[]} profit
 * @return {number}
 */
var jobScheduling = function (startTime, endTime, profit) {
  const n = startTime.length
  const jobs = new Array(n).fill(0).map((_, i) => [startTime[i], endTime[i], profit[i]])
  jobs.sort((a, b) => a[1] - b[1])
  const dp = new Array(n + 1).fill(0)
  const search = (end) => {
    let l = 0
    let r = end
    while (l < r) {
      const mid = ~~((l + r) / 2)
      if (jobs[end][0] >= jobs[mid][1]) {
        l = mid + 1
      } else {
        r = mid
      }
    }
    return l
  }
  for (let i = 1; i <= n; i++) {
    const k = search(i - 1)
    dp[i] = Math.max(dp[i - 1], dp[k] + jobs[i - 1][2])
  }
  return dp[n]
}

• 时间复杂度：$O(n\log{n})$
• 空间复杂度：$O(n)$