困难

问题描述

给定一个由不同正整数的组成的非空数组 nums ，考虑下面的图：

• 有 nums.length 个节点，按从 nums[0] 到 nums[nums.length - 1] 标记；
• 只有当 nums[i] 和 nums[j] 共用一个大于 1 的公因数时，nums[i] 和 nums[j] 之间才有一条边。

返回 图中最大连通组件的大小 。

示例 1：

输入：nums = [4,6,15,35]
输出：4

示例 2：

输入：nums = [20,50,9,63]
输出：2

示例 3：

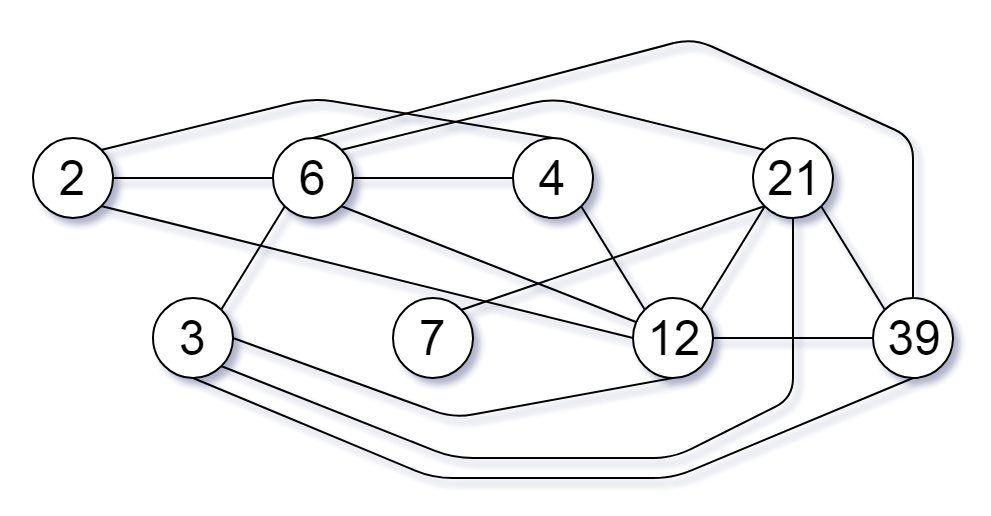
输入：nums = [2,3,6,7,4,12,21,39]
输出：8

提示：

• 1 <= nums.length <= 2 * 104
• 1 <= nums[i] <= 105
• nums 中所有值都 不同

并查集

设 $nums$ 中最大值为 $max$，对应每个不大于 $max$ 的数 $num$， 对于范围 $[2, \sqrt{num}]$ 内的每个正整数 $i$，如果 $i$ 是 $num$ 的因数，则 $num$ 和 $i$、$\dfrac{num}{i}$ 都属于同一个组件。使用并查集实现组件的计算，最终遍历 $nums$ 找出最大的连通组件

/**
 * @param {number[]} nums
 * @return {number}
 */
var largestComponentSize = function (nums) {
  const max = Math.max(...nums)
  const parent = new Array(max + 1).fill(0).map((_, i) => i)
  const find = (x) => {
    if (parent[x] !== x) {
      parent[x] = find(parent[x])
    }
    return parent[x]
  }
  const union = (x, y) => {
    let parentX = find(x)
    let parentY = find(y)
    if (parentX !== parentY) {
      parent[parentX] = parentY
    }
  }
  for (const num of nums) {
    for (let i = 2; i * i <= num; i++) {
      if (num % i === 0) {
        union(num, i)
        union(num, num / i)
      }
    }
  }
  const cnts = new Array(max + 1).fill(0)
  let ans = 0
  for (const num of nums) {
    ans = Math.max(ans, ++cnts[find(num)])
  }
  return ans
}

• 时间复杂度：$O(n\sqrt{m})$，其中 $n$ 为 $nums$ 的长度，$m$ $nums$ 中最大值。
• 空间复杂度：$O(m)$，$m$ 为 $nums$ 中最大值。