困难

问题描述

几乎每一个人都用乘法表。但是你能在乘法表中快速找到第 k 小的数字吗？

给定高度 m 、宽度 n 的一张 m * n 的乘法表，以及正整数 k，你需要返回表中第 k 小的数字。

示例 1：

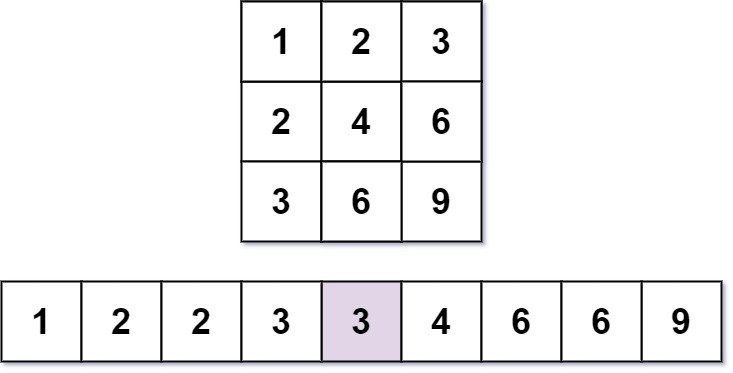
输入: m = 3, n = 3, k = 5
输出: 3
解释: 第 5 小的数字是 3 (1, 2, 2, 3, 3).

示例 2：

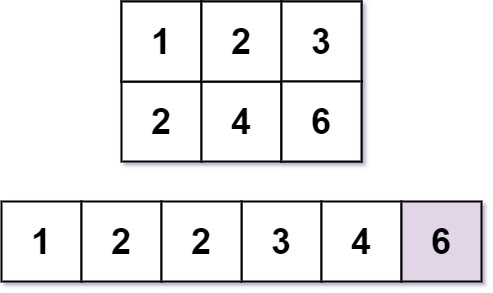
输入: m = 2, n = 3, k = 6
输出: 6
解释: 第 6 小的数字是 6 (1, 2, 2, 3, 4, 6).

提示：

• 1 <= m, n <= 3 * 104
• 1 <= k <= m * n

二分查找

根据题目的约束条件可以知道，$n$ 和 $m$ 可能会很大，求出所有数后再查找第 $k$ 个数会超时。可以转换一下问题：对于乘法表中的数字 $x$，它是乘法表中第几小的数字？

由于乘法表构造性质，决定了乘法表是递增的，第 $i$ 行中，每个数字的是 $i$ 的倍数，因此该行不超过 $x$ 的数有 $min(\lfloor \dfrac{x}{i} \rfloor , n)$ 个，整个乘法表不超过 $x$ 的数字个数为

$$\sum_{i=1}^m {min(\lfloor \dfrac{x}{i} \rfloor , n)}$$

通过二分查找，找出这个刚好是第 $k$ 小的数 $x$ 即可。

/**
 * @param {number} m
 * @param {number} n
 * @param {number} k
 * @return {number}
 */
var findKthNumber = function (m, n, k) {
  const countSmallNum = (num) => {
    let cnt = 0
    for (let i = 1; i <= m; i++) {
      cnt += Math.min(~~(num / i), n)
    }
    return cnt
  }
  let low = 1
  let height = m * n
  while (low < height) {
    const mid = (height + low) >> 1
    const cnt = countSmallNum(mid)
    if (cnt >= k) {
      height = mid
    } else {
      low = mid + 1
    }
  }
  return low
}

• 时间复杂度：$O(m \times log \, mn )$
• 空间复杂度：$O(1)$