中等

问题描述

给定圆的半径和圆心的位置，实现函数 randPoint ，在圆中产生均匀随机点。

实现 Solution 类:

• Solution(double radius, double x_center, double y_center) 用圆的半径 radius 和圆心的位置 (x_center, y_center) 初始化对象
• randPoint() 返回圆内的一个随机点。圆周上的一点被认为在圆内。答案作为数组返回 [x, y]

示例 1：

输入:
["Solution","randPoint","randPoint","randPoint"]
[[1.0, 0.0, 0.0], [], [], []]
输出: [null, [-0.02493, -0.38077], [0.82314, 0.38945], [0.36572, 0.17248]]
解释:
Solution solution = new Solution(1.0, 0.0, 0.0);
solution.randPoint ();//返回[-0.02493，-0.38077]
solution.randPoint ();//返回[0.82314,0.38945]
solution.randPoint ();//返回[0.36572,0.17248]

提示：

• 0 < radius <= 108
• -107 <= x_center, y_center <= 107
• randPoint 最多被调用 3 * 104 次

拒绝采样

这题容易陷入一个误区，随机生成一个 $[-r,r]$ 范围内的随机数 $x$，根据 $x$ 计算出可选的 $y$ 范围区间，再从区间中随机抽取 $y$。实际上，如果按此方法生成随机点，随机点在圆上并非均匀分布的，而是两端密集，中间稀疏。下图是生成 $25000$ 个随机点所得到的图像：

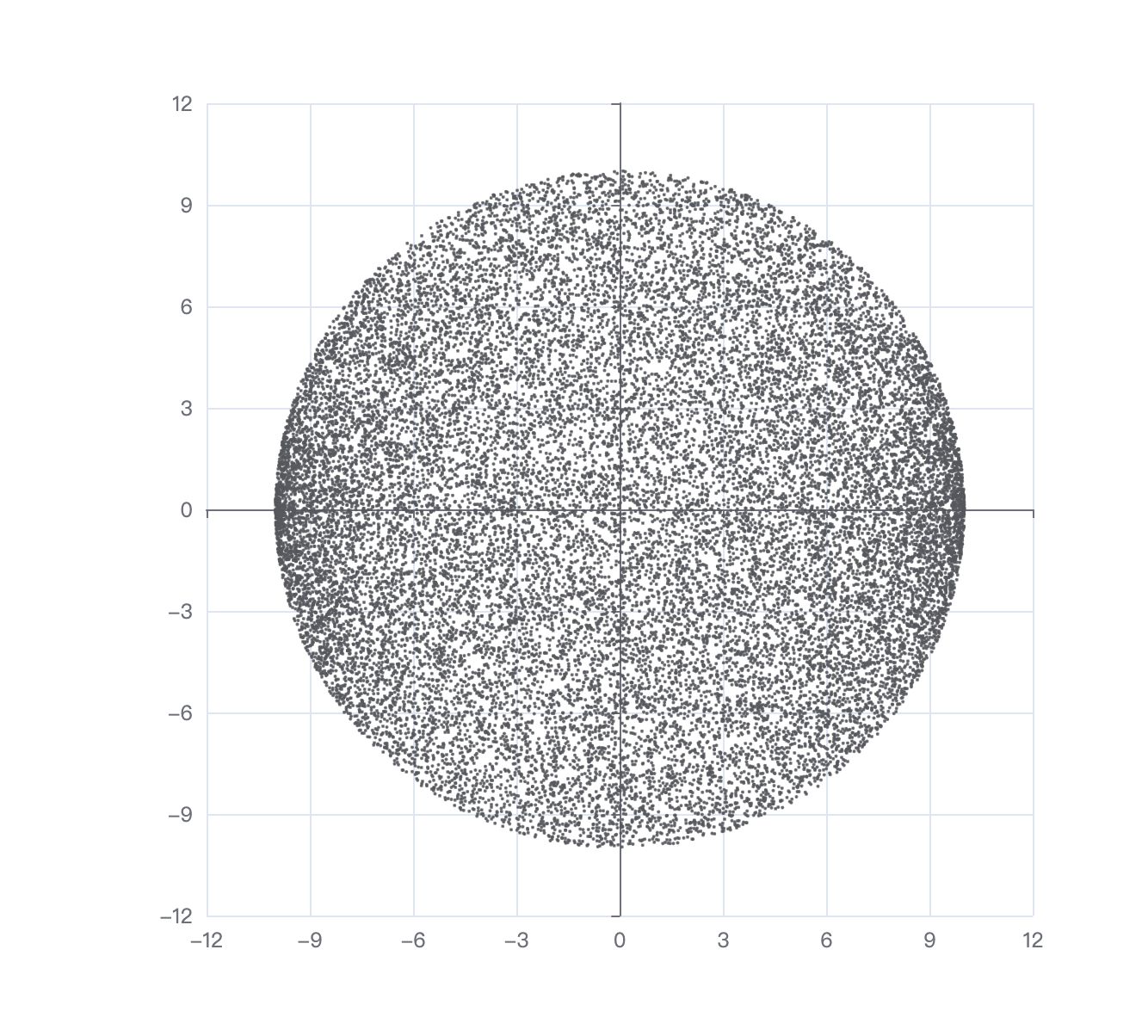
原因在于，选取的 $x$ 是同概率的，但 $x$ 对应的 $y$ 的范围大小是不相同的，离圆心越远的 $y$，可选的范围就越小，假设对应的 $x$ 坐标上有同样多的点存在（相当于 $x$ 随机），越远离圆心，$y$可选的范围就越小，必然会往中间靠拢，就会形成上面两端密集，中间稀疏的图像，不满足均匀的条件。

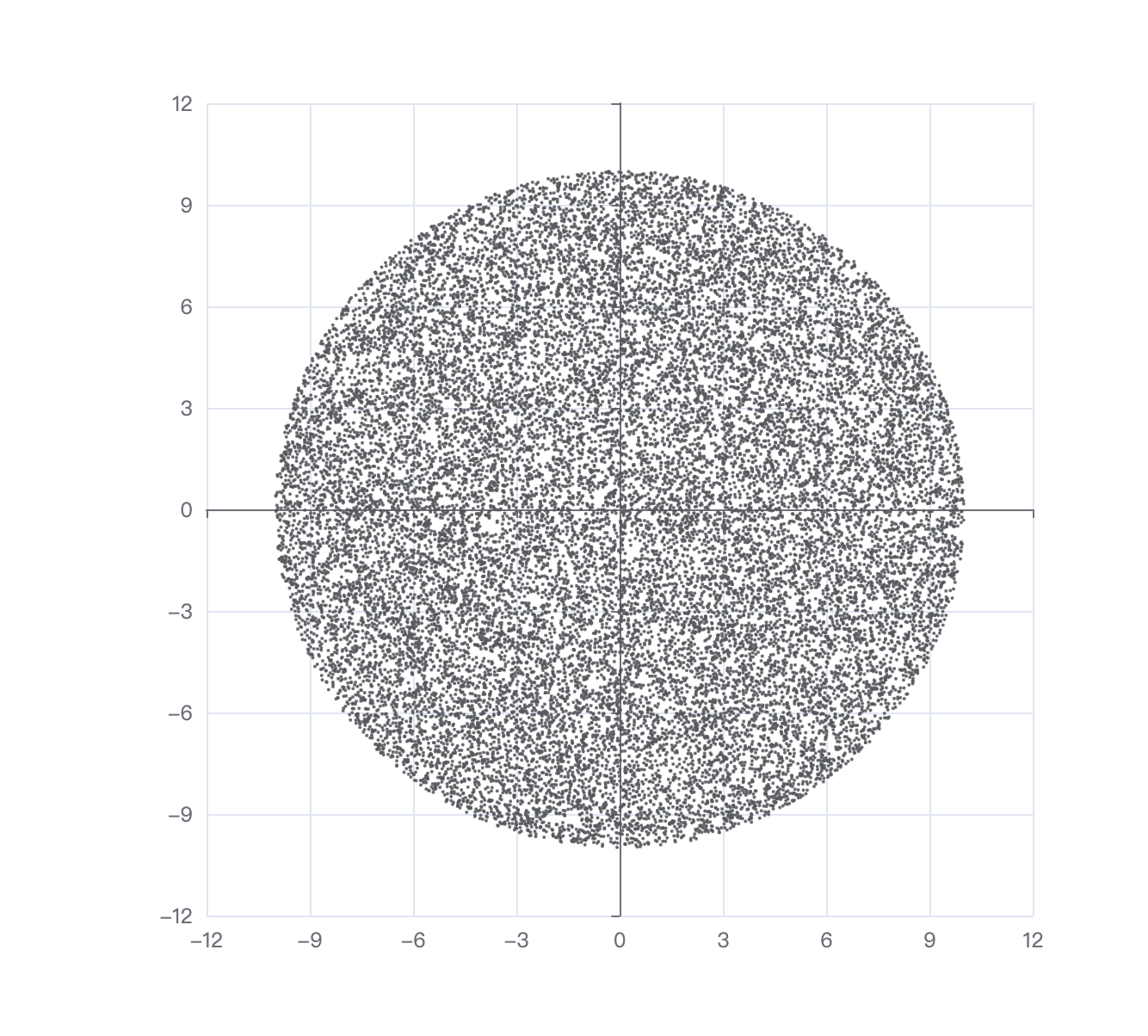
因此，为了避免这种情况，就需要 $y$ 的可选范围不受 $x$ 取值影响，也就 $x$ 和 $y$ 都从 $[-r,r]$ 范围内生成，但这样有概率会落到圆外，处理方法是落到圆外重新生成一个新的坐标，直到生成的坐标落到圆内即可，落到圆内的概率为 $P = \dfrac {\pi r^2}{4r^2} \approx 0.785$，生成坐标落到圆内的数学期望值为 $E = \dfrac {1}{0.785} \approx 1.27$ 。如果在 $[-r,r]$ 的范围内生成随机数，那么是无法生成到横坐标或纵坐标恰好为 $r$ 的点（随机函数区间是左闭右开），即圆周上与正方形边相切的两个点无法随机到，但实际上可以忽略不计。

按此方式生成 $25000$ 个随机点所得到的图像如下：

/**
 * @param {number} radius
 * @param {number} x_center
 * @param {number} y_center
 */
var Solution = function (radius, x_center, y_center) {
  this.r = radius
  this.x = x_center
  this.y = y_center
}

/**
 * @return {number[]}
 */
Solution.prototype.randPoint = function () {
  let r, x, y
  do {
    x = Math.random() * this.r * 2 - this.r
    y = Math.random() * this.r * 2 - this.r
    r = Math.sqrt(x * x + y * y)
  } while (r > this.r)
  return [x + this.x, y + this.y]
}

/**
 * Your Solution object will be instantiated and called as such:
 * var obj = new Solution(radius, x_center, y_center)
 * var param_1 = obj.randPoint()
 */

• 时间复杂度：$O(1)$（期望）
• 空间复杂度：$O(1)$