中等

问题描述

共有 n 名小伙伴一起做游戏。小伙伴们围成一圈，按 顺时针顺序 从 1 到 n 编号。确切地说，从第 i 名小伙伴顺时针移动一位会到达第 (i + 1) 名小伙伴的位置，其中 1 <= i < n ，从第 n 名小伙伴顺时针移动一位会回到第 1 名小伙伴的位置。

游戏遵循如下规则：

1. 从第 1 名小伙伴所在位置 开始 。
2. 沿着顺时针方向数 k 名小伙伴，计数时需要 包含 起始时的那位小伙伴。逐个绕圈进行计数，一些小伙伴可能会被数过不止一次。
3. 你数到的最后一名小伙伴需要离开圈子，并视作输掉游戏。
4. 如果圈子中仍然有不止一名小伙伴，从刚刚输掉的小伙伴的 顺时针下一位 小伙伴 开始，回到步骤 2 继续执行。
5. 否则，圈子中最后一名小伙伴赢得游戏。

给你参与游戏的小伙伴总数 n ，和一个整数 k ，返回游戏的获胜者。

示例 1：

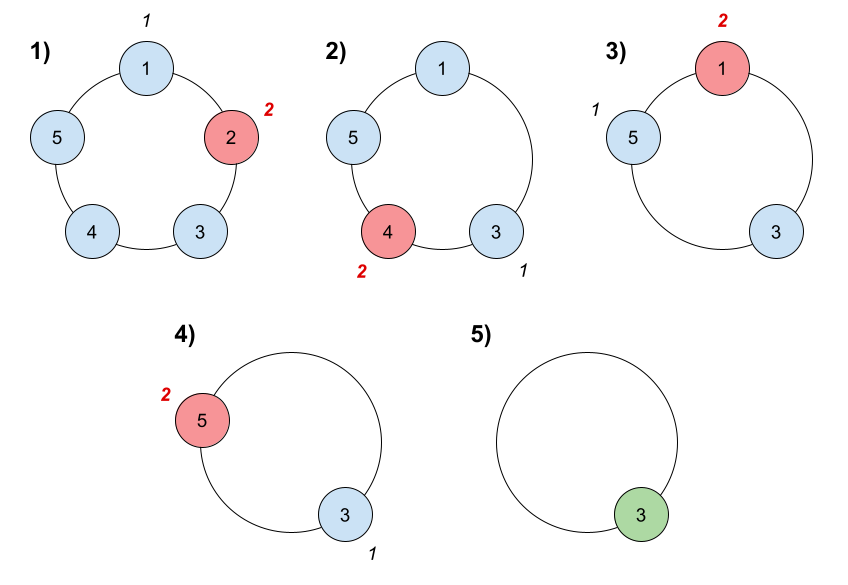
输入：n = 5, k = 2
输出：3
解释：游戏运行步骤如下：
1. 从小伙伴 1 开始。
2. 顺时针数 2 名小伙伴，也就是小伙伴 1 和 2 。
3. 小伙伴 2 离开圈子。下一次从小伙伴 3 开始。
4. 顺时针数 2 名小伙伴，也就是小伙伴 3 和 4 。
5. 小伙伴 4 离开圈子。下一次从小伙伴 5 开始。
6. 顺时针数 2 名小伙伴，也就是小伙伴 5 和 1 。
7. 小伙伴 1 离开圈子。下一次从小伙伴 3 开始。
8. 顺时针数 2 名小伙伴，也就是小伙伴 3 和 5 。
9. 小伙伴 5 离开圈子。只剩下小伙伴 3 。所以小伙伴 3 是游戏的获胜者。

示例 2：

输入：n = 6, k = 5
输出：1
解释：小伙伴离开圈子的顺序：5、4、6、2、3 。小伙伴 1 是游戏的获胜者。

提示：

• 1 <= k <= n <= 500

模拟

通过题目给出的数据范围 $1 <= k <= n <= 500$，可以根据题目给出的规则进行模拟，模拟方法可以使用链表、队列、标记等方法。

以下为标记解法：

创建一个 $vis$ 数组，使用 $vis[i] === true$ 标记数据是否已被淘汰，每次从当前位置 $cur$ 出发，找到第 $k$ 个未被淘汰($vis[i] === false$)的点，将其进行标记 $vis[i] = true$，最终标记出 $n - 1$ 个数据。

代码实现：

/**
 * @param {number} n
 * @param {number} k
 * @return {number}
 */
var findTheWinner = function (n, k) {
  const vis = new Array(n).fill(false)
  let cnt = 0
  let cur = 0
  while (cnt !== n - 1) {
    for (let i = 0; i < k - 1; i++) {
      cur++
      while (vis[cur % n]) cur++
    }
    vis[cur % n] = true
    cnt++
    while (vis[cur % n]) cur++
  }
  return (cur % n) + 1
}

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n)$

约瑟夫环

这同时也是一道约瑟夫环经典题。

设 $f(n, k)$ 表示共有 $n$ 名小伙伴做游戏，计数为 $k$ ，最终获胜者编号，为了便于描述，以下标代替编号从 $0$ 开始

我们采用反推的方法，从最后一轮往回推：

• 最后一轮($n = 1$)，圈子中只有一名小伙伴，该小伙伴即为获胜者，因此 $f(1, k) = 0$。
• 倒数第二轮($n = 2$)，下一轮（$n = 1$）留下的小伙伴在这一轮也会留下，此时它的下标是 $f(2, k) = (0 + k) \% 2$
• 倒数第三轮($n = 3$)，同理可得 $f(3, k) = ((0 + k) \% 2 + k) \% 3$
• $\dots$
• 第一轮，总小伙伴数为 $n$，那么此时它的下标 $f(n, k)$

即

$$f(n,k)= \begin{cases} 0 & n = 1 \\ (f(n-1,k) + k) \% n & n > 1 \\ \end{cases}$$

此处难点在于，为什么$f(n,k) = (f(n-1,k)+k)$

由于获胜者会一直获胜，离开的小伙伴必然是在这个小伙伴之前或之后。由于是一个环，之后其实也可以看成是多转 $N$ 圈后的之前，因此，可以都看成是获胜者之前的小伙伴离开。设获胜者当前下标为$pos'$，上一轮的下标为$pos$，由于在后面轮数中，随着 $n$ 的减少，$k$ 可能大于当前的 $n$，所以，为了确保离开的小伙伴下标在前面，我们 $k$ 倍当前的 $n$ 地扩大数组下标，由于反推上一轮操作可以看成是插入了一个小伙伴，扩大了 $k$ 倍当前的 $n$ ，相当于插入了 $k$ 个相同的小伙伴，所以有$pos = pos' + k * n + k$，计算出上一轮的坐标后，由于是扩大了的结果，$pos$ 可能会大于 $n$，此时对 $pos$ 进行缩小，就有 $pos \% n = (pos' + k * n + k) \% n = (pos' + k) \% n$

实现代码：

• 时间复杂度：$O(n)$
• 空间复杂度：忽略递归带来的额外空间开销，复杂度为$O(1)$