简单

问题描述

有一个具有 n 个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 source 开始，到顶点 destination 结束的 有效路径 。

给你数组 edges 和整数 n、source 和 destination，如果从 source 到 destination 存在 有效路径 ，则返回 true，否则返回 false 。

示例 1：

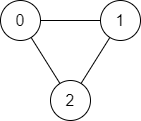
输入：n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
输出：true
解释：存在由顶点 0 到顶点 2 的路径:
- 0 → 1 → 2
- 0 → 2

示例 2：

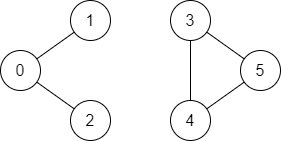
输入：n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
输出：false
解释：不存在由顶点 0 到顶点 5 的路径.

提示：

• 1 <= n <= 2 * 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ui, vi <= n - 1
• ui != vi
• 0 <= source, destination <= n - 1
• 不存在重复边
• 不存在指向顶点自身的边

广度优先搜索

首先通过 $edges$ 构造出双向图 $graph$，再从点 $source$ 出发，进行广度优先搜索，搜索过程中若遇到点 $destination$，则说明存在有效路径，返回 $true$，若搜索完毕后仍未找到点 $destination$，则返回 $false$。

/**
 * @param {number} n
 * @param {number[][]} edges
 * @param {number} source
 * @param {number} destination
 * @return {boolean}
 */
var validPath = function (n, edges, source, destination) {
  if (source === destination) return true
  const graph = new Array(n).fill(0).map(() => new Array())
  for (const edge of edges) {
    graph[edge[0]].push(edge[1])
    graph[edge[1]].push(edge[0])
  }
  let queue = [source]
  const visited = new Set()
  while (queue.length) {
    const node = queue.shift()
    for (const point of graph[node]) {
      if (visited.has(point)) continue
      if (point === destination) return true
      queue.push(point)
      visited.add(point)
    }
  }
  return false
}

• 时间复杂度：$O(n + m)$，其中 $n$ 表示图中顶点的数目，$m$ 表示图中边的数目。
• 空间复杂度：$O(n + m)$，其中 $n$ 表示图中顶点的数目，$m$ 表示图中边的数目。

并查集

可以先构建并查集，然后对每条边的两个节点进行合并，最后查询 $source$ 和 $destination$ 是否存在相同的祖先，若相同则说明存在有效路径。

/**
 * @param {number} n
 * @param {number[][]} edges
 * @param {number} source
 * @param {number} destination
 * @return {boolean}
 */
var validPath = function (n, edges, source, destination) {
  const parents = new Array(n).fill(0).map((_, i) => i)
  const find = (x) => {
    if (parents[x] !== x) {
      parents[x] = find(parents[x])
    }
    return parents[x]
  }
  const union = (x, y) => {
    const parentX = find(x)
    const parentY = find(y)
    if (parentX !== parentY) {
      parents[parentX] = parentY
    }
  }
  for (const edge of edges) {
    union(...edge)
  }
  return find(source) === find(destination)
}

• 时间复杂度：$O(n + m \times \alpha(m))$，其中 $n$ 表示图中顶点的数目，$m$ 表示图中边的数目，$\alpha$ 是反阿克曼函数。
• 空间复杂度：$O(n)$，其中 $n$ 表示图中顶点的数目。