困难

问题描述

在无限长的数轴（即 x 轴）上，我们根据给定的顺序放置对应的正方形方块。

第 i 个掉落的方块（positions[i] = (left, side_length)）是正方形，其中 left 表示该方块最左边的点位置(positions[i][0])，side_length 表示该方块的边长(positions[i][1])。

每个方块的底部边缘平行于数轴（即 x 轴），并且从一个比目前所有的落地方块更高的高度掉落而下。在上一个方块结束掉落，并保持静止后，才开始掉落新方块。

方块的底边具有非常大的粘性，并将保持固定在它们所接触的任何长度表面上（无论是数轴还是其他方块）。邻接掉落的边不会过早地粘合在一起，因为只有底边才具有粘性。

返回一个堆叠高度列表 ans 。每一个堆叠高度 ans[i] 表示在通过 positions[0], positions[1], ..., positions[i] 表示的方块掉落结束后，目前所有已经落稳的方块堆叠的最高高度。

示例 1:

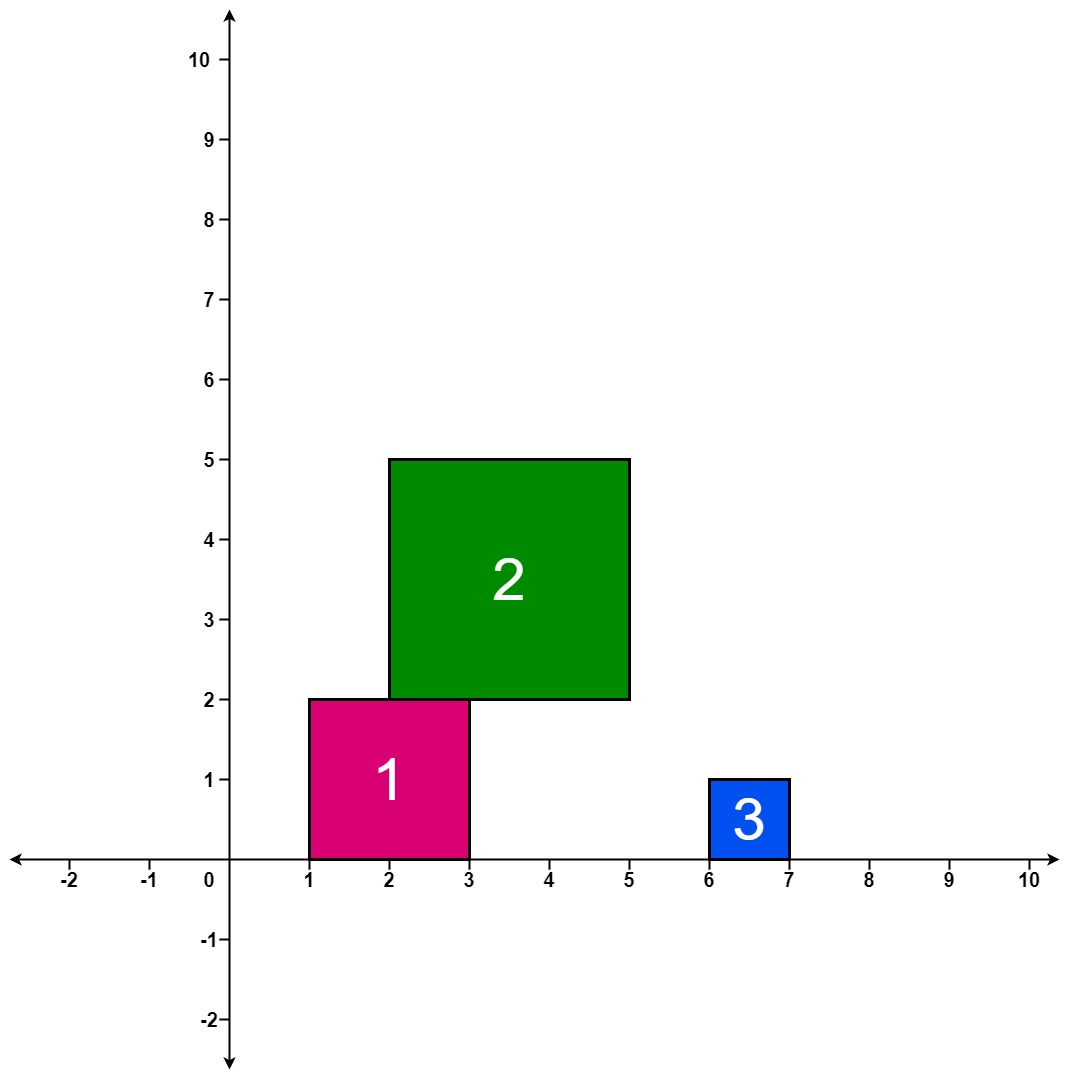
输入: [[1, 2], [2, 3], [6, 1]]
输出: [2, 5, 5]
解释:
第一个方块 positions[0] = [1, 2] 掉落后，方块最大高度为 2。
第二个方块 positions[1] = [2, 3] 掉落后，大的方块保持在较小的方块的顶部，不论它的重心在哪里，因为方块的底部边缘有非常大的粘性，所以方块最大高度为 5。
第三个方块 positions[1] = [6, 1] 掉落后，方块的最大高度仍然是第一个和第二个方块堆叠成的高度 5。
因此，我们返回结果[2, 5, 5]。

示例 2:

输入: [[100, 100], [200, 100]]
输出: [100, 100]
解释: 相邻的方块不会过早地卡住，只有它们的底部边缘才能粘在表面上。

提示:

• 1 <= positions.length <= 1000
• 1 <= positions[i][0] <= 108
• 1 <= positions[i][1] <= 106

暴力枚举

我们可以模拟整个过程，使用一个数组 $blocks$ 记录每一个方块的位置和它的堆叠高度，使用一个变量 $maxHeight$ 记录当前方块堆叠的最大高度。遍历每一个方块，然后遍历所有 $blocks$ 中的记录，如果当前方块与 $blocks$ 中的当前记录出现堆叠，则更新当前模块的堆叠高度，最终方块的位置信息与得到的高度记录到 $blocks$ 记录表中。如果当前方块的堆叠高度大于历史最大堆叠高度，则更新最大堆叠高度，把当前最大堆叠高度记录到 $ans$ 中。

/**
 * @param {number[][]} positions
 * @return {number[]}
 */
var fallingSquares = function (positions) {
  const ans = []
  const blocks = []
  let maxHeight = 0
  for (const [start, size] of positions) {
    let height = size
    for (const [l, r, h] of blocks) {
      if (!(start + size <= l || start >= r)) {
        height = Math.max(height, h + size)
      }
    }
    maxHeight = Math.max(maxHeight, height)
    blocks.push([start, start + size, height])
    ans.push(maxHeight)
  }
  return ans
}

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$