简单

问题描述

环形公交路线上有 n 个站，按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离，distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。

环线上的公交车都可以按顺时针和逆时针的方向行驶。

返回乘客从出发点 start 到目的地 destination 之间的最短距离。

示例 1：

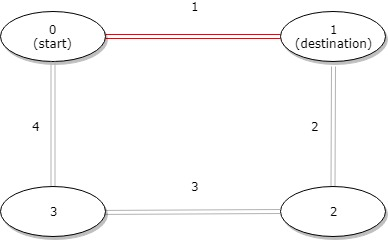
输入：distance = [1,2,3,4], start = 0, destination = 1
输出：1
解释：公交站 0 和 1 之间的距离是 1 或 9，最小值是 1。

示例 2：

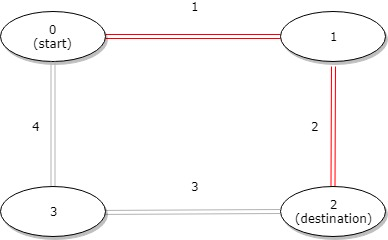
输入：distance = [1,2,3,4], start = 0, destination = 2
输出：3
解释：公交站 0 和 2 之间的距离是 3 或 7，最小值是 3。

示例 3：

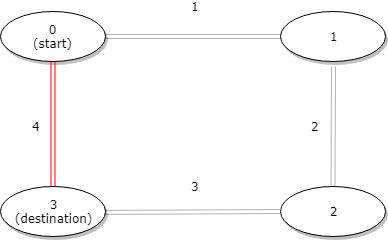
输入：distance = [1,2,3,4], start = 0, destination = 3
输出：4
解释：公交站 0 和 3 之间的距离是 6 或 4，最小值是 4。

提示：

• 1 <= n <= 104
• distance.length == n
• 0 <= start, destination < n
• 0 <= distance[i] <= 104

一次遍历

从起点到终点只有顺时针和逆时针两种走法，分别统计两种走法的距离，取最小值即可，注意的是，若起点位置大于终点位置，可以等价看作从终点到起点。

/**
 * @param {number[]} distance
 * @param {number} start
 * @param {number} destination
 * @return {number}
 */
var distanceBetweenBusStops = function (distance, start, destination) {
  if (start > destination) return distanceBetweenBusStops(distance, destination, start)
  let sum1 = 0
  let sum2 = 0
  for (let i = 0; i < distance.length; i++) {
    if (i >= start && i < destination) {
      sum1 += distance[i]
    } else {
      sum2 += distance[i]
    }
  }
  return Math.min(sum1, sum2)
}

• 时间复杂度：$O(n)$。
• 空间复杂度：$O(1)$。