中等

问题描述

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

示例 1:

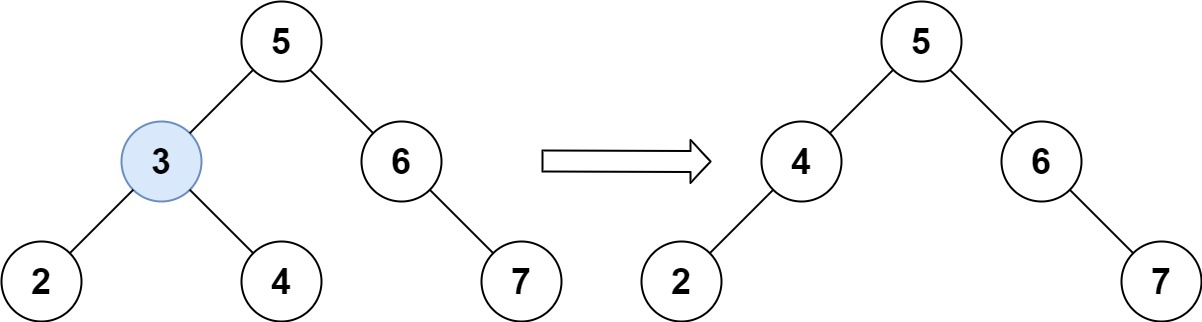
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
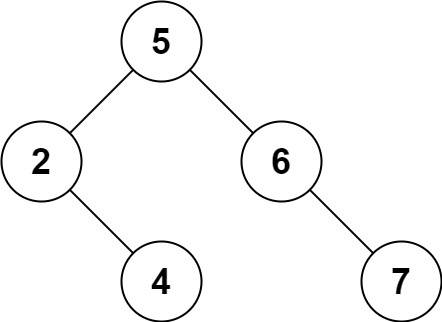
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

提示:

• 节点数的范围 [0, 104]
• -105 <= Node.val <= 105
• 节点值唯一
• root 是合法的二叉搜索树
• -105 <= key <= 105

进阶：要求算法时间复杂度为 O(h)，h 为树的高度。

递归

二叉搜索树具有以下性质：

• 左子树的所有节点（如果有）的值均小于当前节点的值；
• 右子树的所有节点（如果有）的值均大于当前节点的值；
• 左子树和右子树均为二叉搜索树。

利用二叉搜索树的性质，可以递归去搜索值为 $key$ 的节点：

• 如果 $root$ 为空，搜索到树的底部都未能找到值为 $key$ 的节点，返回空。
• 如果 $root.val > key$，说明值为 $key$ 的节点可能在左子树中，将 $root.left$ 作为新的根节点，调用 $deleteNode$，让它在左子树中寻找值为 $key$ 的节并执行删除操作，将删除节点后的子树作为新的左子树。
• 如果 $root.val < key$，说明值为 $key$ 的节点可能在右子树中，将 $root.right$ 作为新的根节点，调用 $deleteNode$，让它在右子树中寻找值为 $key$ 的节并执行删除操作，将删除节点后的子树作为新的右子树。
• 如果 $root.val = key$，说明已经找到了需要删除的目标节点，要进行删除操作，因为递归的上层逻辑会将返回值作为新的子树，所以我们返回新的根节点就相当于删除了目标节点：
  • 如果目标节点的左子树为空，则返回右子树。
  • 如果目标节点的右子树为空，则返回左子树。
  • 如果左右子树都不为空，删除节点后，需要重新调整节点位置，因为二叉搜索树的性质，左子树节点的值必然小于右子树，如果左右子树合并，需要将左子树变成右子树值最小的节点的左子树，右子树值最小的节点就是右子树最左的节点，合并后返回右子树；或者将右子树变成左子树值最大的节点的右子树，左子树值最大的节点就是左子树最右的节点，合并后返回左子树。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} key
 * @return {TreeNode}
 */
var deleteNode = function (root, key) {
  if (!root) return null
  if (root.val === key) {
    if (!root.left) return root.right
    if (!root.right) return root.left
    let node = root.right
    while (node.left) {
      node = node.left
    }
    node.left = root.left
    return root.right
  } else if (root.val > key) {
    root.left = deleteNode(root.left, key)
  } else {
    root.right = deleteNode(root.right, key)
  }
  return root
}

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

迭代

迭代跟递归也是相同的原理，为了方便，我们可以构造一个哨兵节点，将输入的搜索二叉树作为哨兵节点的左子树，最终返回哨兵节点的左节点即可。

因为删除目标节点，我们需要修改的是目标节点的父节点的左节点或右节点的指向，我们将递归是判断当前节点的值是否跟目标值相同改为判断当前节点的左节点或右节点的值是否跟目标值相同，找到目标节点后的逻辑基相同，就不再赘述了。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} key
 * @return {TreeNode}
 */
var deleteNode = function (root, key) {
  if (!root) return null
  const head = new TreeNode(Infinity, root, null)
  const queue = [head]
  while (queue.length) {
    const parent = queue.shift()
    let target = null
    if (parent.left && parent.left.val === key) {
      target = parent.left
    } else if (parent.right && parent.right.val === key) {
      target = parent.right
    }
    if (target) {
      let node = null
      if (!target.left) {
        node = target.right
      } else if (!target.right) {
        node = target.left
      } else {
        node = target.right
        while (node.left) {
          node = node.left
        }
        node.left = target.left
        node = target.right
      }
      if (parent.left === target) {
        parent.left = node
      } else {
        parent.right = node
      }
    } else {
      if (parent.left && parent.val > key) queue.push(parent.left)
      if (parent.right && parent.val < key) queue.push(parent.right)
    }
  }
  return head.left
}

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$