LC 675. 为高尔夫比赛砍树 (opens new window) (opens new window)

困难

# 问题描述

你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个 m x n 的矩阵表示，在这个矩阵中：

0 表示障碍，无法触碰
1 表示地面，可以行走
比 1 大的数表示有树的单元格，可以行走，数值表示树的高度

每一步，你都可以向上、下、左、右四个方向之一移动一个单位，如果你站的地方有一棵树，那么你可以决定是否要砍倒它。

你需要按照树的高度从低向高砍掉所有的树，每砍过一颗树，该单元格的值变为 1（即变为地面）。

你将从 (0, 0) 点开始工作，返回你砍完所有树需要走的最小步数。如果你无法砍完所有的树，返回 -1 。

可以保证的是，没有两棵树的高度是相同的，并且你至少需要砍倒一棵树。

示例 1：

示例 1

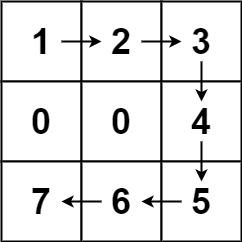
输入：forest = [[1,2,3],[0,0,4],[7,6,5]]
输出：6
解释：沿着上面的路径，你可以用 6 步，按从最矮到最高的顺序砍掉这些树。

示例 2：

示例 2

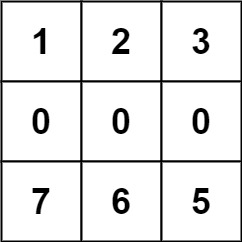
输入：forest = [[1,2,3],[0,0,0],[7,6,5]]
输出：-1
解释：由于中间一行被障碍阻塞，无法访问最下面一行中的树。

示例 3：

输入：forest = [[2,3,4],[0,0,5],[8,7,6]]
输出：6
解释：可以按与示例 1 相同的路径来砍掉所有的树。
(0,0) 位置的树，可以直接砍去，不用算步数。

提示：

m == forest.length
n == forest[i].length
1 <= m, n <= 50
0 <= forest[i][j] <= 10⁹

# 广度优先搜索

题目需要从矮到高的顺序去砍树，那么我们先遍历一次矩阵，获取到所有树的坐标，然后按树的高度进行排序，然后依次求出相邻两棵树的最短距离。

求相邻两棵树的最短距离我们可以使用广度优先搜索，按层次遍历。用队列 $queue$ 用于记录当层需要走的点，数组 $visited$ 记录已被处理或在队列中待处理的点。我们对队列中的点进行处理，查找它们四个方向上的点，如果相邻的点是在矩阵中，且不是不可达（非 $0$ ），且未被数组 $visited$ 记录，则添加到下一层队列中，直到到找到终点（下一棵树的位置），返回当前步数。若不能到达，则返回 $-1$ 。由于是按层次去遍历的，最先到达终点的步数必然是最少步数，最少步数的和就算整体步数的最少值，最终如果每棵树都能到达，则返回他们步数之和，若某棵树不可达，则返回 $-1$ 。

/**
 * @param {number[][]} forest
 * @return {number}
 */
var cutOffTree = function (forest) {
  const rows = forest.length
  const cols = forest[0].length
  const dirs = [
    [-1, 0],
    [1, 0],
    [0, -1],
    [0, 1]
  ]
  const trees = []
  for (let i = 0; i < rows; i++) {
    for (let j = 0; j < cols; j++) {
      if (forest[i][j] > 1) {
        trees.push([i, j])
      }
    }
  }
  trees.sort((a, b) => forest[a[0]][a[1]] - forest[b[0]][b[1]])
  const bfs = (sx, sy, ex, ey) => {
    let step = 0
    if (sx === ex && sy === ey) return step
    const visited = new Array(rows).fill(0).map(() => new Array(cols))
    let queue = [[sx, sy]]
    visited[sx][sy] = true
    while (queue.length) {
      step++
      const newQueue = []
      for (const [x, y] of queue) {
        for (const dir of dirs) {
          const nx = x + dir[0]
          const ny = y + dir[1]
          if (nx === ex && ny === ey) return step
          if (nx > -1 && nx < rows && ny > -1 && ny < cols) {
            if (forest[nx][ny] !== 0 && !visited[nx][ny]) {
              newQueue.push([nx, ny])
              visited[nx][ny] = true
            }
          }
        }
      }
      queue = newQueue
    }
    return -1
  }
  let sx = 0
  let sy = 0
  let ans = 0
  for (const tree of trees) {
    const step = bfs(sx, sy, tree[0], tree[1])
    if (step === -1) return -1
    ans += step
    ;[sx, sy] = tree
  }
  return ans
}

时间复杂度： $O(m^2 \times n^2)$
空间复杂度： $O(m \times n)$

# Dijkstra 算法

也可以使用 $\text {Dijkstra}$ 算法求相邻两棵树的最短距离。 $\text {Dijkstra}$ 算法也是利用的广度优先搜索，只是每次对队列中优先选择最短路径的元素。写法上区别并不大，因为相邻节点的距离固定是 1，无需像广度优先搜索构建新的队列，直接入队即可。

$\text {JavaScript}$ 没有提供优先队列，但是 $\text {LeetCode}$ 提供了 $\text {MinPriorityQueue}$ 和 $\text {MaxPriorityQueue}$ ，可以直接使用^[1]

/**
 * @param {number[][]} forest
 * @return {number}
 */
var cutOffTree = function (forest) {
  const rows = forest.length
  const cols = forest[0].length
  const dirs = [
    [-1, 0],
    [1, 0],
    [0, -1],
    [0, 1]
  ]
  const trees = []
  for (let i = 0; i < rows; i++) {
    for (let j = 0; j < cols; j++) {
      if (forest[i][j] > 1) {
        trees.push([i, j])
      }
    }
  }
  trees.sort((a, b) => forest[a[0]][a[1]] - forest[b[0]][b[1]])
  const bfs = (sx, sy, ex, ey) => {
    if (sx === ex && sy === ey) return 0
    const visited = new Array(rows).fill(0).map(() => new Array(cols))
    const queue = new MinPriorityQueue({ priority: (i) => i[0] })
    queue.enqueue([0, sx, sy])
    visited[sx][sy] = true
    while (queue.size()) {
      const [step, x, y] = queue.dequeue().element
      for (const dir of dirs) {
        const nx = x + dir[0]
        const ny = y + dir[1]
        if (nx === ex && ny === ey) return step + 1
        if (nx > -1 && nx < rows && ny > -1 && ny < cols) {
          if (forest[nx][ny] !== 0 && !visited[nx][ny]) {
            queue.enqueue([step + 1, nx, ny])
            visited[nx][ny] = true
          }
        }
      }
    }
    return -1
  }
  let sx = 0
  let sy = 0
  let ans = 0
  for (const tree of trees) {
    const step = bfs(sx, sy, tree[0], tree[1])
    if (step === -1) return -1
    ans += step
    ;[sx, sy] = tree
  }
  return ans
}

时间复杂度： $O(m^2 \times n^2 \times log(m \times n))$
空间复杂度： $O(m \times n)$

# A* 启发式搜索算法^[2]

$\text{A*}$ 算法是另一种路径查找算法，设 $\text{A*}$ 的估算函数为 $f(x, y) = g(x, y) + h(x, y)$ ，其中 $g(x, y)$ 表示从起点 ( $sx$ , $sy$ ) 到 ( $x$ , $y$ ) 的实际距离，评估函数 $h(x, y)$ 选择 $(x, y)$ 到 $(ex, ey)$ 的曼哈顿距离。

与 $\text {Dijkstra}$ 算法不同， $\text {Dijkstra}$ 算法队列中的点已经是与当前节点最近的点，后续在遇到相同节点时，步数不可能更少，因此需要标记，无需再次进队，但 $\text {A*}$ 算法队列中的点是预估可能是最近的点，假设我们是要从起点 $S$ 到终点 $T$ ，且当前位于中途点 $x$ ，中途点 $x$ 最少步数的预估包括两部分： 起点 $S$ 到中途点 $x$ 的步数 和 从中途点 $x$ 到终点 $T$ 的理论最少步数（曼哈顿距离），起点 $S$ 到中途点 $x$ 的步数实际上有可能并非是实际最少步数，如果遇到起点 $S$ 到中途点 $x$ 更少的步数时，需要其进行再次入队，才能确保得到最短路径。

/**
 * @param {number[][]} forest
 * @return {number}
 */
var cutOffTree = function (forest) {
  const rows = forest.length
  const cols = forest[0].length
  const dirs = [
    [-1, 0],
    [1, 0],
    [0, -1],
    [0, 1]
  ]
  const trees = []
  for (let i = 0; i < rows; i++) {
    for (let j = 0; j < cols; j++) {
      if (forest[i][j] > 1) {
        trees.push([i, j])
      }
    }
  }
  trees.sort((a, b) => forest[a[0]][a[1]] - forest[b[0]][b[1]])
  const md = (x1, y1, x2, y2) => Math.abs(x1 - x2) + Math.abs(y1 - y2)
  const bfs = (sx, sy, ex, ey) => {
    if (sx === ex && sy === ey) return 0
    const steps = new Array(rows).fill(0).map(() => new Array(cols).fill(-1))
    const queue = new MinPriorityQueue({ priority: (i) => i[0] })
    queue.enqueue([md(sx, sy, ex, ey), 0, sx, sy])
    steps[sx][sy] = 0
    while (queue.size()) {
      const [_, step, x, y] = queue.dequeue().element
      for (const dir of dirs) {
        const nx = x + dir[0]
        const ny = y + dir[1]
        if (nx === ex && ny === ey) return step + 1
        if (nx > -1 && nx < rows && ny > -1 && ny < cols) {
          if (forest[nx][ny] !== 0) {
            if (steps[nx][ny] === -1 || step + 1 < steps[nx][ny]) {
              const cost = step + 1 + md(nx, ny, ex, ey)
              queue.enqueue([cost, step + 1, nx, ny])
              steps[nx][ny] = step + 1
            }
          }
        }
      }
    }
    return -1
  }
  let sx = 0
  let sy = 0
  let ans = 0
  for (const tree of trees) {
    const step = bfs(sx, sy, tree[0], tree[1])
    if (step === -1) return -1
    ans += step
    ;[sx, sy] = tree
  }
  return ans
}

时间复杂度：启发式搜索不讨论空复杂度
空间复杂度：启发式搜索不讨论空复杂度

#启发式搜索 #图论 #数组 #矩阵 #优先队列

上次更新: 2023/01/31 19:48:05

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

← LC 672. 灯泡开关 II LC 676. 实现一个魔法字典 →

LC 675. 为高尔夫比赛砍树 (opens new window) (opens new window)

# 问题描述

# 广度优先搜索

# Dijkstra 算法

# A* 启发式搜索算法[2]

# A* 启发式搜索算法^[2]