困难

问题描述

病毒扩散得很快，现在你的任务是尽可能地通过安装防火墙来隔离病毒。

假设世界由 m x n 的二维矩阵 isInfected 组成， isInfected[i][j] == 0 表示该区域未感染病毒，而 isInfected[i][j] == 1 表示该区域已感染病毒。可以在任意 2 个相邻单元之间的共享边界上安装一个防火墙（并且只有一个防火墙）。

每天晚上，病毒会从被感染区域向相邻未感染区域扩散，除非被防火墙隔离。现由于资源有限，每天你只能安装一系列防火墙来隔离其中一个被病毒感染的区域（一个区域或连续的一片区域），且该感染区域对未感染区域的威胁最大且 保证唯一 。

你需要努力使得最后有部分区域不被病毒感染，如果可以成功，那么返回需要使用的防火墙个数; 如果无法实现，则返回在世界被病毒全部感染时已安装的防火墙个数。

示例 1：

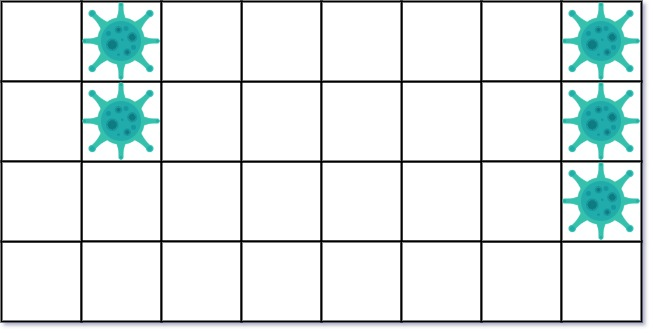
输入: isInfected = [[0,1,0,0,0,0,0,1],[0,1,0,0,0,0,0,1],[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0]]
输出: 10
解释:一共有两块被病毒感染的区域。
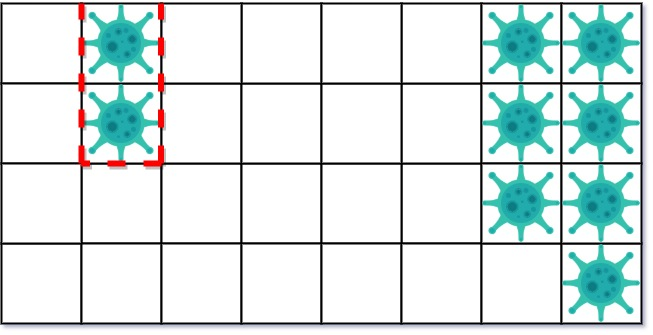
在第一天，添加 5 墙隔离病毒区域的左侧。病毒传播后的状态是:

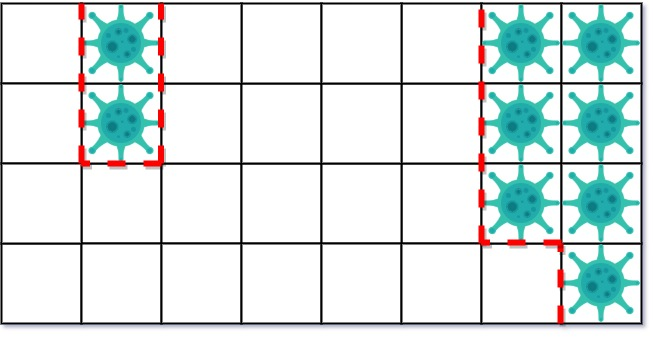
第二天，在右侧添加 5 个墙来隔离病毒区域。此时病毒已经被完全控制住了。

示例 2：

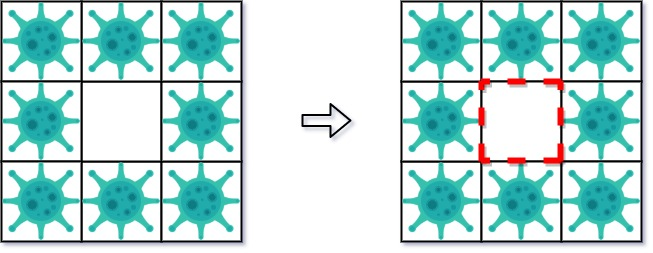
输入: isInfected = [[1,1,1],[1,0,1],[1,1,1]]
输出: 4
解释: 虽然只保存了一个小区域，但却有四面墙。
注意，防火墙只建立在两个不同区域的共享边界上。

示例 3:

输入: isInfected = [[1,1,1,0,0,0,0,0,0],[1,0,1,0,1,1,1,1,1],[1,1,1,0,0,0,0,0,0]]
输出: 13
解释: 在隔离右边感染区域后，隔离左边病毒区域只需要 2 个防火墙。

提示:

• m == isInfected.length
• n == isInfected[i].length
• 1 <= m, n <= 50
• isInfected[i][j] 不是 0 就是 1
• 在整个描述的过程中，总有一个相邻的病毒区域，它将在下一轮 严格地感染更多未受污染的方块

广度优先搜索

对矩阵进行遍历，当遇到 $1$ 时，从当前位置开始，进行广度优先搜索，获取到一块连续的病毒感染区域，并将区域 打上标记，把区域内的值全部赋值为 $-idx(idx \geq 1)$。由于还需要查找相邻未感染区域的个数和记录防火墙的个数，所以再广度优先搜索过程中，如果遇到未感染区域（即 $0$）,则将该区域记录下来，同时防火墙数量加 $1$。由于查找到的未感染区域可能会重复，所以使用集合来记录。

当找到所有感染区域后，从这些感染区域找到「对未感染区域的威胁最大」的区域，即相邻未感染区域最多的区域，优先将它隔离起来，将该区域隔离需要使用的防火墙个数累加到答案中，同时将区域赋值为 $2$，表示该区域已被隔离，下次查找连续的病毒感染区域时跳过该区域。其他未隔离的区域重置为 $1$，且相邻的未感染区域也置为 $1$，之后重新查找下一个病毒感染区域。当没有找到下一个病毒感染区域或者当前已经是最后一个病毒感染区时结束对感染区的查找。

const DIRS = [
  [-1, 0],
  [1, 0],
  [0, -1],
  [0, 1]
]
/**
 * @param {number[][]} isInfected
 * @return {number}
 */
var containVirus = function (isInfected) {
  const m = isInfected.length
  const n = isInfected[0].length
  let ans = 0
  while (true) {
    const neighbours = []
    const firewalls = []
    for (let i = 0; i < m; i++) {
      for (let j = 0; j < n; j++) {
        if (isInfected[i][j] === 1) {
          const neighbour = new Set()
          let firewall = 0
          const idx = neighbours.length + 1
          const queue = [[i, j]]
          isInfected[i][j] = -idx
          while (queue.length) {
            const [x, y] = queue.shift()
            for (const dir of DIRS) {
              const $x = x + dir[0]
              const $y = y + dir[1]
              if (-1 < $x && $x < m && -1 < $y && $y < n) {
                if (isInfected[$x][$y] === 1) {
                  queue.push([$x, $y])
                  isInfected[$x][$y] = -idx
                } else if (isInfected[$x][$y] === 0) {
                  firewall++
                  neighbour.add(`${$x},${$y}`)
                }
              }
            }
          }
          neighbours.push(neighbour)
          firewalls.push(firewall)
        }
      }
    }
    if (neighbours.length === 0) break
    let idx = 0
    for (let i = 1; i < neighbours.length; i++) {
      if (neighbours[i].size > neighbours[idx].size) idx = i
    }
    ans += firewalls[idx]
    for (let i = 0; i < m; i++) {
      for (let j = 0; j < n; j++) {
        if (isInfected[i][j] < 0) {
          if (isInfected[i][j] === -(idx + 1)) isInfected[i][j] = 2
          else isInfected[i][j] = 1
        }
      }
    }
    for (let i = 0; i < neighbours.length; i++) {
      if (i !== idx) {
        for (const neighbour of neighbours[i]) {
          const [x, y] = neighbour.split(',').map((i) => +i)
          isInfected[x][y] = 1
        }
      }
    }
    if (neighbours.length === 1) break
  }
  return ans
}

• 时间复杂度：$O((n + m) \times n \times m)$
• 空间复杂度：$O(n \times m)$