简单

问题描述

给你一个 m x n 的矩阵，最开始的时候，每个单元格中的值都是 0。

另有一个二维索引数组 indices，indices[i] = [ri, ci] 指向矩阵中的某个位置，其中 ri 和 ci 分别表示指定的行和列（从 0 开始编号）。

对 indices[i] 所指向的每个位置，应同时执行下述增量操作：

• ri 行上的所有单元格，加 1 。
• ci 列上的所有单元格，加 1 。

给你 m、n 和 indices 。请你在执行完所有 indices 指定的增量操作后，返回矩阵中 奇数值单元格 的数目。

示例 1：

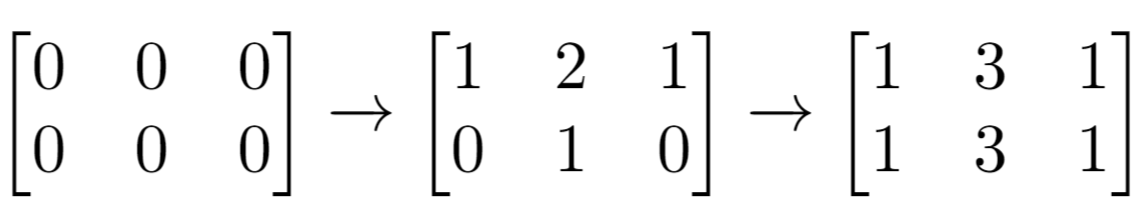
输入：m = 2, n = 3, indices = [[0,1],[1,1]]
输出：6
解释：最开始的矩阵是 [[0,0,0],[0,0,0]]。
第一次增量操作后得到 [[1,2,1],[0,1,0]]。
最后的矩阵是 [[1,3,1],[1,3,1]]，里面有 6 个奇数。

示例 2：

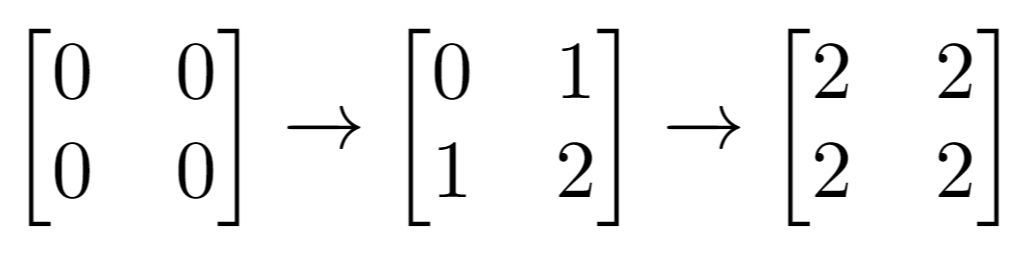
输入：m = 2, n = 2, indices = [[1,1],[0,0]]
输出：0
解释：最后的矩阵是 [[2,2],[2,2]]，里面没有奇数。

提示：

• 1 <= m, n <= 50
• 1 <= indices.length <= 100
• 0 <= ri < m
• 0 <= ci < n

进阶：你可以设计一个时间复杂度为 O(n + m + indices.length) 且仅用 O(n + m) 额外空间的算法来解决此问题吗？

模拟

建立两个数组，分别记录对应行 $rows$ 和列 $cols$ 加 $1$ 的次数，最后枚举行列所记录的次数，若同时为奇数或同时为偶数时，该位置最终得到的数必然是偶数，只有当行列所记录的互为奇偶，最终得到的才会是奇数，最终返回行列互为奇偶的个数即可。由于只涉及奇偶数，因此可以用异或运算替代。

/**
 * @param {number} m
 * @param {number} n
 * @param {number[][]} indices
 * @return {number}
 */
var oddCells = function (m, n, indices) {
  const rows = new Array(m).fill(0)
  const cols = new Array(n).fill(0)
  for (const [row, col] of indices) {
    rows[row] ^= 1
    cols[col] ^= 1
  }
  let ans = 0
  for (const row of rows) {
    for (const col of cols) {
      ans += row ^ col
    }
  }
  return ans
}

• 时间复杂度：$O(q \times n \times m)$，其中 $q$ 表示数组 $indices$ 的长度，$m$, $n$ 为矩阵的行数与列数。
• 空间复杂度：$O(n + m)$，$m$, $n$ 为矩阵的行数与列数。