中等

问题描述

给定一个二叉树的根 root 和两个整数 val 和 depth ，在给定的深度 depth 处添加一个值为 val 的节点行。

注意，根节点 root 位于深度 1 。

加法规则如下:

• 给定整数 depth，对于深度为 depth - 1 的每个非空树节点 cur ，创建两个值为 val 的树节点作为 cur 的左子树根和右子树根。
• cur 原来的左子树应该是新的左子树根的左子树。
• cur 原来的右子树应该是新的右子树根的右子树。
• 如果 depth == 1 意味着 depth - 1 根本没有深度，那么创建一个树节点，值 val 作为整个原始树的新根，而原始树就是新根的左子树。

示例 1:

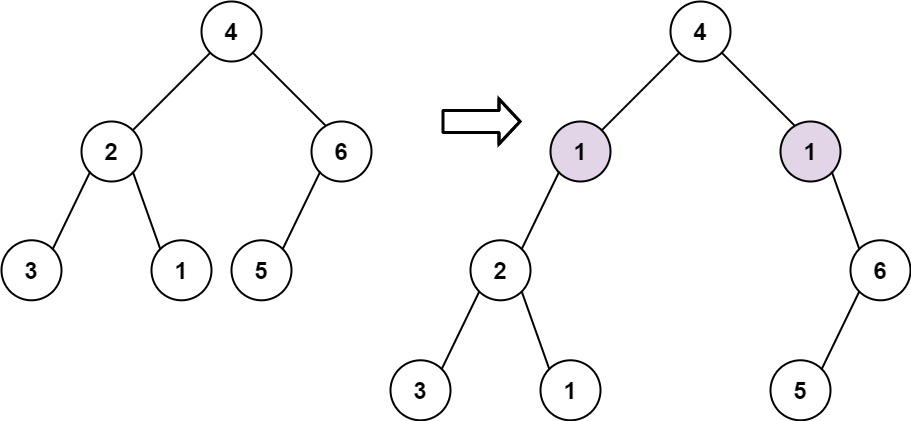
输入: root = [4,2,6,3,1,5], val = 1, depth = 2
输出: [4,1,1,2,null,null,6,3,1,5]

示例 2:

输入: root = [4,2,null,3,1], val = 1, depth = 3
输出: [4,2,null,1,1,3,null,null,1]

提示:

• 节点数在 [1, 104] 范围内
• 树的深度在 [1, 104] 范围内
• -100 <= Node.val <= 100
• -105 <= val <= 105
• 1 <= depth <= the depth of tree + 1

广度优先搜索

• 当 $depth = 1$ 时，创建一个新的 $TreeNode$ 节点，其左子树为 $root$ 节点，返回新的$TreeNode$ 节点。
• 当 $depth > 1$ 时，对树进行一次层次遍历获取第 $depth - 1$ 层节点，然后遍历该层的节点 $node$，每个节点左右子树都插入一个新的 $TreeNode$ 节点，位于左子树的 $TreeNode$ 的左子树指向 $node$ 原有的左子树，位于右子树的 $TreeNode$ 的右子树指向 $node$ 原有的右子树，最后返回 $root$ 节点。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} val
 * @param {number} depth
 * @return {TreeNode}
 */
var addOneRow = function (root, val, depth) {
  if (depth === 1) {
    return new TreeNode(val, root)
  } else {
    let level = 1
    let queue = [root]
    while (++level < depth) {
      const q = []
      for (const node of queue) {
        if (node.left) q.push(node.left)
        if (node.right) q.push(node.right)
      }
      queue = q
    }
    for (const node of queue) {
      node.left = new TreeNode(val, node.left)
      node.right = new TreeNode(val, null, node.right)
    }
    return root
  }
}

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$